热烈祝贺博士研究生李志远作为第一作者在《Computer Methods in Applied Mechanics and Engineering》发表了题为“Peridynamic operator method”的研究论文!
本文提出了近场动力学算子方法(Peridynamic operator method, PDOM)。该方法可将局部微分及其乘积转化为相应的非局部积分形式。近场动力学微分算子(Peridynamic differential operator, PDDO)和非局部算子方法(Nonlocal operator method,NOM)可视为本方法的特例。采用变分原理和拉格朗日方程,推导了PDOM弹性模型。当限定积分域为球形时,该弹性模型可简化为所有类型的近场动力学(Peridynamics,PD)和对偶域近场动力学(Dual-horizon Peridynamics,DH-PD)模型。本方法可简单有效地建立无零能模式的非局部模型,且无需特殊处理间断点与奇异点。通过在离散数据与偏微分方程等方面的应用验证了本方法的能力。
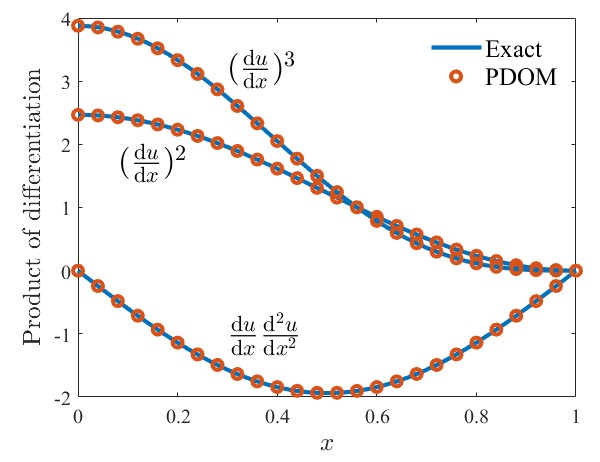
图1 一维离散数据的微分乘积对比
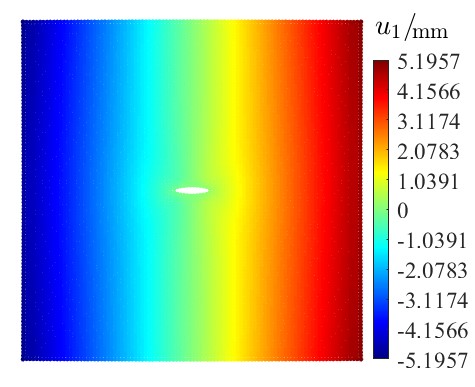
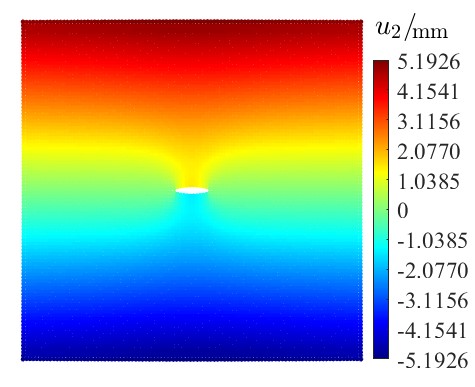
图2 含裂纹板拉伸的位移分布 (左) 水平位移 (右) 竖直位移
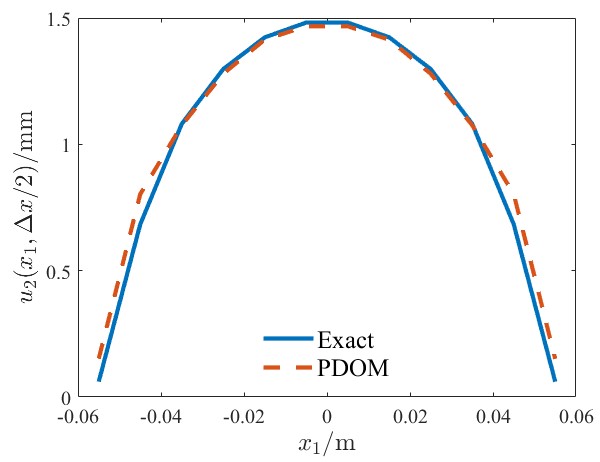
图3 裂纹开口位移对比