近场动力学(Peridynamics, PD)方法作为一种积分型非局部理论，在处理不连续问题中表现出传统数值计算方法不可比拟的独特优势。但由于其建模思路与传统局部模型联系不紧密，大大增加了模拟其他物理现象的建模难度。近场动力学算子类方法的出现逐渐改善了这一现状，如近场动力学微分算子(Peridynamic differential operator, PDDO)，非局部算子方法(Nonlocal operator method, NOM)，键关联的PDDO弱形式(Weak form of bond-associated peridynamic differential operator, WBA-PDDO)和近场动力学算子方法(Peridynamic operator method, PDOM)。    

◉  PDDO

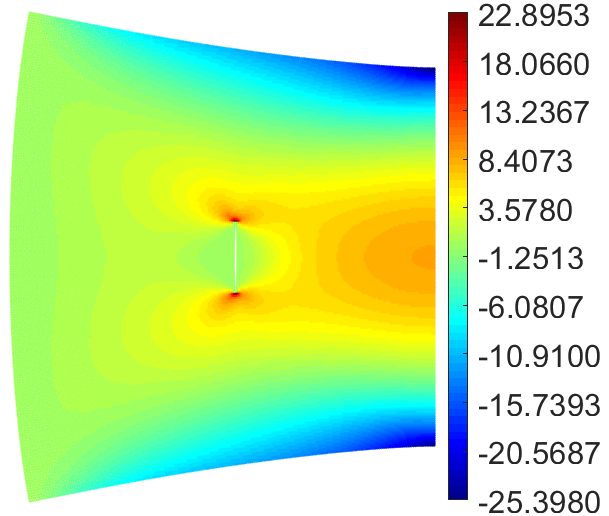
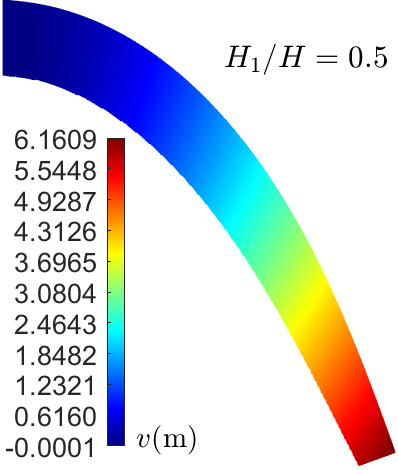
                       功能梯度含裂纹板热应力                                  功能梯度变厚度梁大变形                                    固液相变 

◉  WBA-PDDO

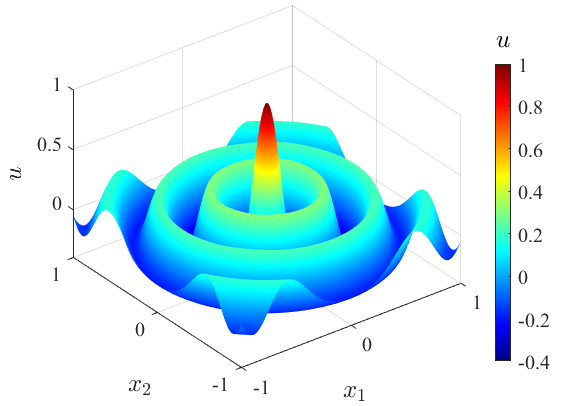
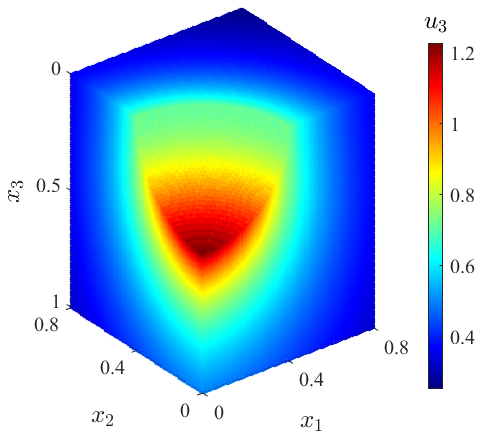
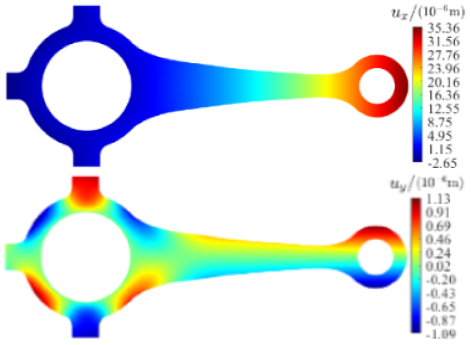
                               亥姆霍兹方程                                            布西内斯克问题                                   正交各向异性连杆热致变形      

◉  PDOM

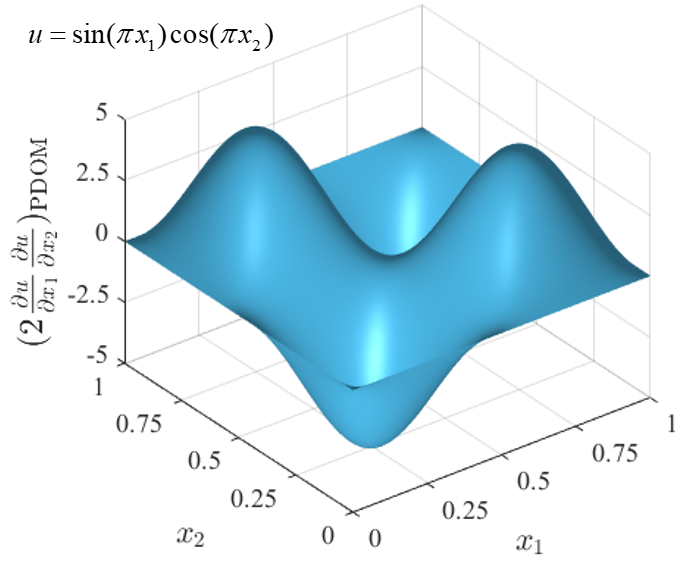
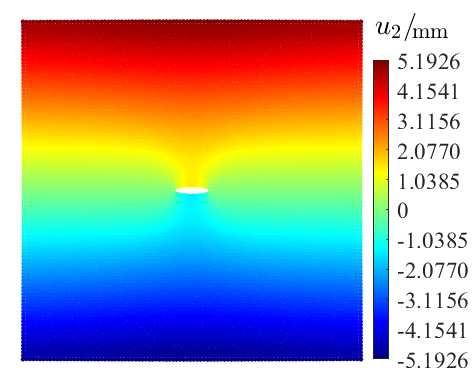
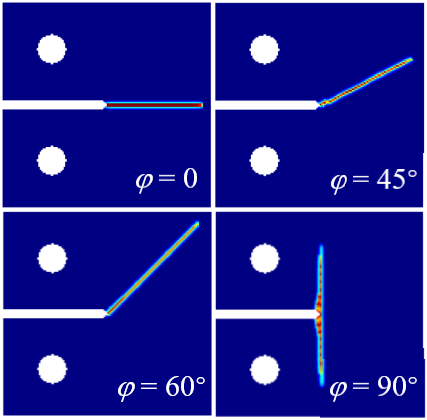
           微分乘积的近似                                     含裂纹板双轴拉伸                                         各向异性断裂